Каждая СУБД поддерживает определенные виды и типы данных, а также средства представления связей между данными, составляющими модель данных. Хранимые в базе данные должны иметь определенную логическую структуру, которая описывается некоторой даталогической моделью данных, поддерживаемой СУБД.

Как уже отмечалось, даталогические модели делятся на документальные и фактографические. В этой главе речь будет идти о фактографических моделях, служащих для описания хорошо структурированных данных.

В литературе и в обиходной речи иногда понятия «модель данных» и «модель базы данных» («схема базы данных») используются как синонимы. Однако это неверно, на что указывают многие авторитетные специалисты, в том числе К. Дж. Дейт, М. Р. Когаловский, С. Д. Кузнецов. Модель данных есть теория, или инструмент моделирования, в то время как модель базы данных (схема базы данных) есть результат моделирования. По выражению К. Дейта соотношение между этими понятиями аналогично соотношению между языком программирования и конкретной программой на этом языке.

Модель данных – это совокупность правил порождения структур данных в базе данных, операций над ними, а также ограничений целостности, определяющих допустимые связи и значения данных, последовательность их изменения.

Любая модель данных должна содержать три компонента:

Структуру данных
Набор допустимых операций, выполняемых на структуре данных.
Ограничения целостности.

Структуры данных

Все данные размещаются в некоторой структуре для обеспечения информационных потребностей пользователей. Здесь можно провести аналогию с языками программирования, в которых тоже есть типы структур данных, такие как массивы, записи и т.д.

Определим основные структуры даталогических моделей данных.

Элемент данных – наименьшая поименованная единица данных, к которой СУБД может обращаться непосредственно и с помощью которой выполняется построение всех остальных структур. Для каждого элемента данных должен быть определён его тип. В разных СУБД могут использоваться разные типы данных, наиболее распространенными из которых являются следующие: целый (integer), символьный (char), дата (date) и т.д.

Запись – поименованная совокупность полей.

Файл – поименованная совокупность экземпляров записей одного типа.

Набор допустимых операций

Такими операциями являются: создание и модификация структур данных, внесение новых данных, удаление и модификация существующих данных, поиск данных по различным условиям. Модель данных предполагает, как минимум, наличие языка определения данных (DDL – Data Definition Language), описывающего структуру их хранения, и языка манипулирования данными (DML – Data Manipulation Language), включающего операции извлечения и модификации данных.

Ограничения целостности

Ограничения целостности – механизм поддержания соответствия данных предметной области на основе формально описанных правил. Правила целостности определяются типом данных и предметной областью. Например, значение поля Количество товара является целым числом. А ограничения предметной области таковы, что это число не может быть меньше нуля.

В процессе исторического развития в СУБД использовались следующие модели данных: иерархическая, сетевая, реляционная. Эти модели отличаются между собой по способу установления связей между данными.

2. Иерархическая модель данных

Первая информационная система, использующая базы данных, появилась в середине шестидесятых годов и была основана на иерархической модели. Иерархическая модель – модель данных, в которой связи между данными имеют вид иерархий. Такую модель можно описать с помощью упорядоченного графа (или дерева) с дугамисвязями и узлами-элементами данных. Иерархическая структура предполагала неравноправие между данными — одни жестко подчинены другим.

На рис. 1 показан пример иерархической модели данных.

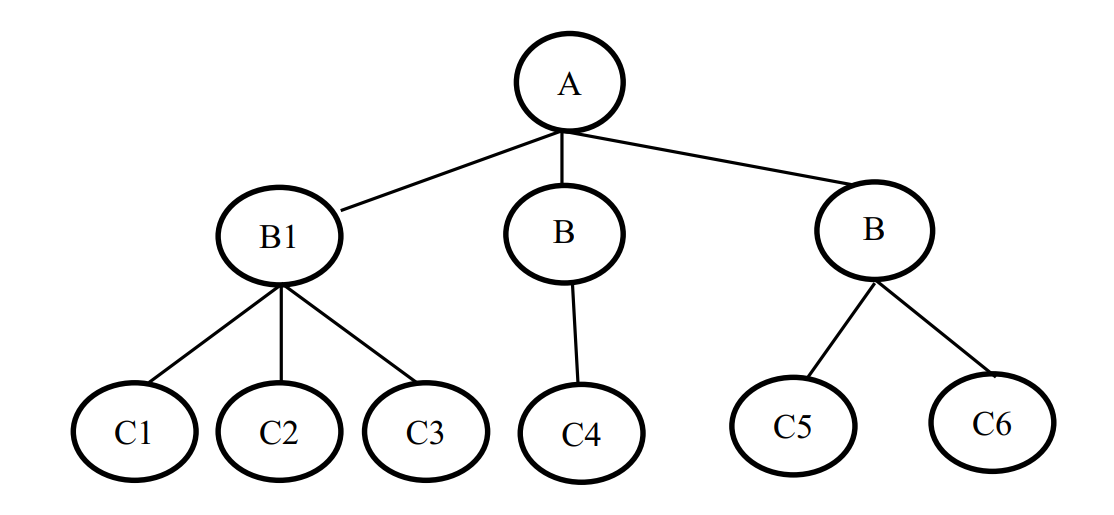
Рис. 1. Пример иерархической модели данных

Дерево представляет собой иерархию элементов, называемых узлами. В иерархической модели имеется корневой узел или просто корень дерева. Корень находится на самом верхнем уровне и не имеет узлов, стоящих выше него. У одного дерева может быть только один корень. Остальные узлы называются порожденными и связаны между собой следующим образом: каждый узел имеет исходный, находящийся на более высоком уровне.

Если каждый узел может быть связан только с одним исходным узлом, то на последующем уровне он может иметь один, два и больше узлов либо не иметь ни одного. В последнем случае узлы, не имеющие порожденных узлов, называются листьями. Доступ к порожденным узлам возможен только через исходный узел, поэтому существует только один путь доступа к каждому узлу.

Появление иерархической модели связано с тем, что в реальном мире очень многие связи соответствуют иерархии, когда один объект выступает как родительский, а с ним может быть связано множество подчиненных объектов.

Основными информационными единицами в иерархической модели являются: атрибут, сегмент и групповое отношение.

Атрибут данных (элемент данных, поле) определяется как минимальная, неделимая единица данных, доступная пользователю с помощью СУБД. Обычно каждому элементу при описании базы данных присваивается уникальное имя. По этому имени к нему обращаются при обработке. Элемент данных также часто называют полем.

Сегмент в терминологии Американской Ассоциации по базам данных DBTG (Data Base Task Group) называется записью, при этом в рамках иерархической модели определяются два понятия: тип сегмента (тип записи) и экземпляр сегмента (экземпляр записи). Тип сегмента определяется составом ее атрибутов. Экземпляр записи — конкретная запись с конкретным значением элементов. Каждый тип сегмента в рамках иерархической модели образует некоторый набор однородных записей. Использование записей позволяет за одно обращение к базе получить некоторую логически связанную совокупность данных. Именно записи изменяются, добавляются и удаляются.

Групповое отношение — иерархическое отношение между записями двух типов. Родительская запись (владелец группового отношения) называется исходной записью, а дочерние записи (члены группового отношения) — подчиненными. Иерархическая база данных может хранить только такие древовидные структуры.

В иерархической модели сегменты объединяются в ориентированный древовидный граф — дерево. При этом полагают, что направленные ребра графа отражают иерархические связи между сегментами.

Корневая запись каждого дерева обязательно должна содержать ключ с уникальным значением. Ключи некорневых записей должны иметь уникальное значение только в рамках группового отношения. Каждая запись идентифицируется полным сцепленным ключом, под которым понимается совокупность ключей всех записей от корневой по иерархическому пути.

Схема иерархической БД представляет собой совокупность отдельных деревьев, содержащих экземпляры типа «запись» (записи). Поля записей хранят значения разных типов данных, составляющие основное содержание БД. Обход всех элементов иерархической БД обычно производится сверху вниз и слева направо.

В качестве примера рассмотрим модель данных организации (рис. 2). Организация состоит из отделов, в которых работают сотрудники, и филиалов. В каждом отделе может работать несколько сотрудников, но сотрудник не может работать более чем в одном отделе.

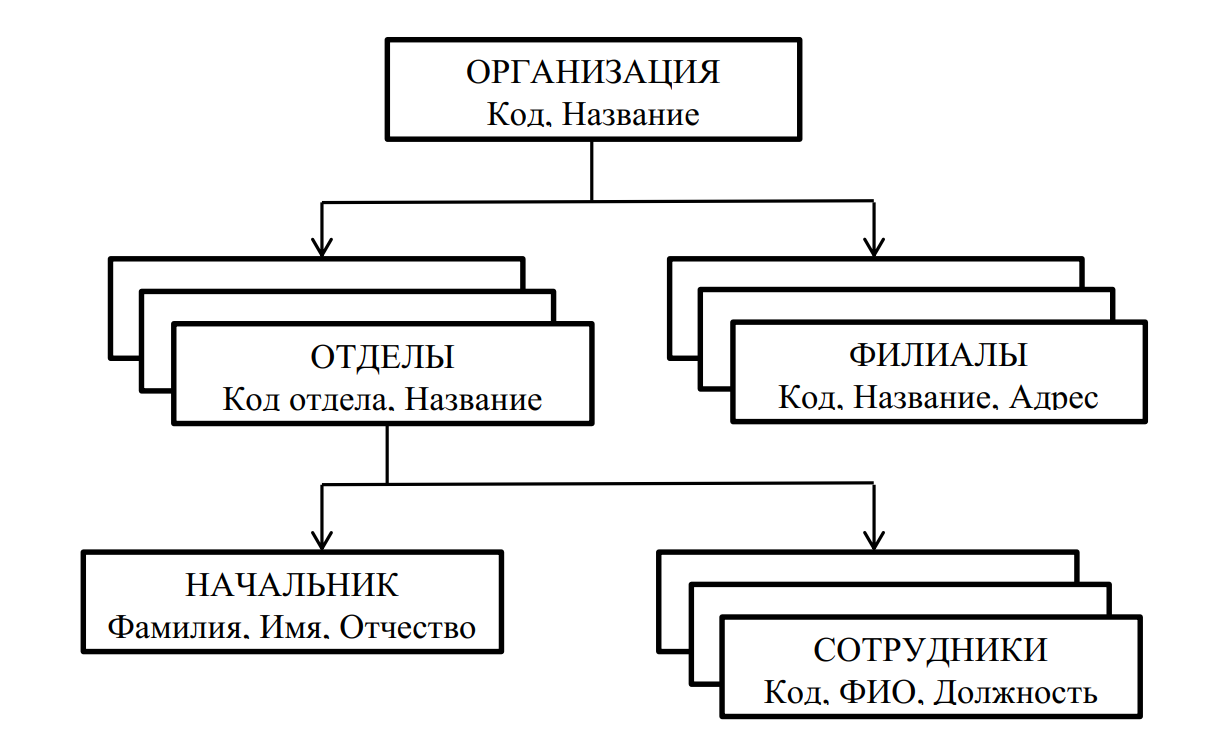
Рис. 2. Иерархическая модель данных организации

К основным операциям манипулирования иерархически организованными данными относятся следующие:

Добавить в базу данных новую запись. Для корневой записи обязательно формирование значения ключа.
Изменить значение данных предварительно извлеченной записи. Ключевые данные не должны подвергаться изменениям.
Удалить некоторую запись и все подчиненные ей записи.
Извлечь корневую запись по ключевому значению, допускается также последовательный просмотр корневых записей.
Извлечь следующую запись (следующая запись извлекается в порядке левостороннего обхода дерева).

В соответствии с определением типа «дерево», можно заключить, что между предками и потомками автоматически поддерживается контроль целостности связей. Основное правило контроля целостности формулируется следующим образом: потомок не может существовать без родителя, а у некоторых родителей может не быть потомков. Механизмы поддержания целостности связей между записями различных деревьев отсутствуют.

К достоинствам иерархической модели данных относятся:

эффективное использование памяти ЭВМ;
высокая скорость выполнения основных операций над данными;
удобство работы с иерархически упорядоченной информацией.

К основным недостаткам такого вида модели можно отнести следующие:

громоздкость для обработки информации с достаточно сложными логическими связями;
иерархия в значительной степени усложняет операции включения информации о новых объектах в базе данных и удаления устаревших. Так при удалении экземпляров исходного узла автоматически удаляются все экземпляры порожденных узлов.
исключительно навигационный принцип доступа к данным.

3. Сетевая модель данных

Прежде чем перейти к рассмотрению сетевой модели данных рассмотрим следующий пример: предприятие со сборочным характером производства выпускает множество изделий, которые включают в себя детали-сборочные единицы (ДСЕ), которые можно разделить на две группы:

уникальные ДСЕ, входящие только в одно изделие или только в одну сборочную единицу;
ДСЕ общего применения, которые могут входить в несколько изделий или других ДСЕ (например, гайки, винты, шайбы и т.п.).

В этом случае взаимосвязь между объектами показана на рис. 3, откуда видно, что данная схема не является иерархической, так как порожденный элемент ДСЕ4 имеет два исхода.

Такие отношения между объектами, в которых порожденный элемент имеет более одного исходного, описываются в виде сетевой структуры. Отличительная черта сетевой структуры от иерархической заключается в том, что любой элемент в сетевой структуре может быть связан с любым другим элементом.

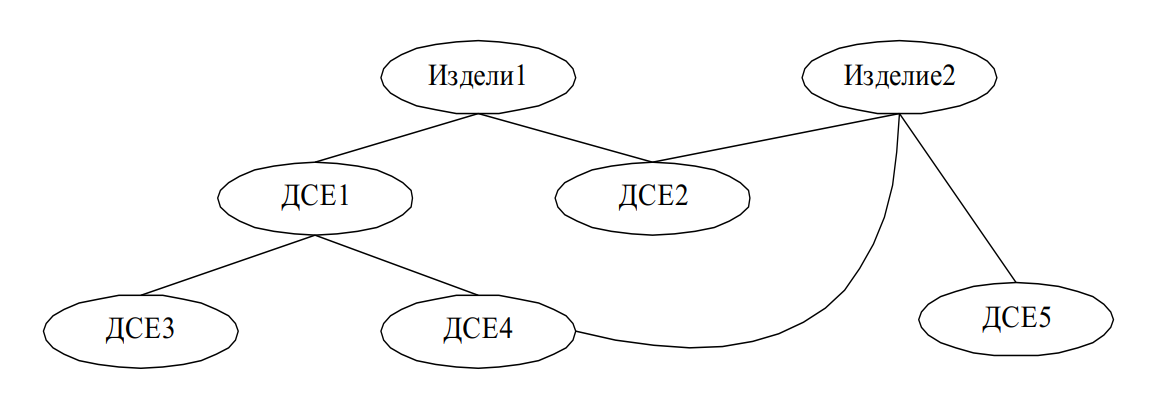
Рис. 3. Пример сетевой модели данных

Таким образом, сетевая модель данных позволяет отображать разнообразные взаимосвязи элементов данных в виде произвольного графа, обобщая тем самым иерархическую модель данных. Стандарт сетевой модели впервые был определен в 1971 году организацией CODASYL (Conference of Data System Languages), которая определила базовые понятия модели и формальный язык описания.

Сетевая модель данных определяется в тех же терминах, что и иерархическая. Она состоит из набора записей и набора соответствующих связей. На формирование связи особых ограничений не накладывается. Если в иерархических структурах запись-потомок могла иметь только одну запись-предка, то в сетевой модели данных запись-потомок может иметь произвольное число записей-предков (сводных родителей).

Реализация групповых отношений (связей) в сетевой модели осуществляется с использованием специально вводимых дополнительных полей — указателей (адресов связи или ссылок), которые устанавливают связь между владельцем и членом группового отношения. Запись может состоять в отношениях разных типов (один-к одному 1:1, один-ко-многим 1:М, много-ко многим M:М).

Заметим, что если один из вариантов установления связи 1:1 очевиден (в запись — владелец отношения включается дополнительное поле – указатель на запись – член отношения), то возможность представления связей 1:М и M:М таким же образом весьма проблематична. Поэтому наиболее распространенным способом организации связей в сетевых СУБД является введение дополнительного типа записей (и соответственно, дополнительного файла), полями которых являются указатели.

К числу важнейших операций манипулирования данными баз сетевого типа можно отнести следующие:

поиск записи в БД;
переход от предка к первому потомку;
переход от потомка к предку;
создание новой записи;
удаление текущей записи;
обновление текущей записи;
включение записи в связь;
исключение записи из связи;
изменение связей и т. д.

В сравнении с иерархической моделью сетевая модель предоставляет большие возможности в смысле допустимости образования произвольных связей.

Основной недостаток сетевой модели состоит в ее сложности и жесткости схемы БД. Прикладной программист должен детально знать логическую структуру базы данных, поскольку ему необходимо осуществлять навигацию среди различных экземпляров и записей.

Другим недостатком является ослабленный контроль за целостностью связей вследствие допустимости установления произвольных связей между записями.

Пользуясь популярной в технологической сфере терминологией, базы данных, использующие иерархические и сетевые модели данных можно отнести к базам данных первого поколения. Основным способом работы с базами данных этих типов являлся так называемый «навигационный» способ, заключающийся в перемещении по графу, описывающему структуру базы данных, и низкоуровневой поэлементной обработке содержащихся в узлах этого графа структур данных.

Основным недостатком баз данных первого поколения являлась сложность структуры данных даже для достаточно простых систем, что приводило к сложности прикладных программ обработки данных, требующих детального описания навигационных путей к данным.

Кроме того, наличие в программах навигационных путей крайне затрудняло модификацию структуры данных, поскольку требовало модификации всех соответствующих программ обработки. Это, в свою очередь, практически не давало возможности разделить функции проектировщика данных и проектировщика прикладных программ, что являлось заметным препятствием при реализации больших проектов.

Поворотным пунктом в теории и практике баз данных явился переход к реляционным базам данных.

4. Реляционная модель данных

Отмеченные выше недостатки иерархических и сетевых моделей данных обусловлены, главным образом, тем, что в этих моделях записи связаны между собой с помощью указателей.

Указатель – это физический адрес, обозначающий место хранения записи на диске. Достоинство указателей состоит в том, что они позволяют быстро извлекать данные, которые связаны между собой. Недостаток заключается в том, что эти связи должны быть определены при проектировании базы данных. Извлечь данные на основе других связей сложно, если вообще возможно. В то же время введение новых связей приводило к изменению всей модели данных и базы данных в целом.

В 1970 году Э. Кодд (E. Codd) опубликовал статью, в которой выдвинул идею о том, что данные нужно связывать не физическими указателями, а в соответствии с их внутренними логическими взаимоотношениями. Таким образом, пользователи смогут комбинировать данные из разных источников на основе логических зависимостей между ними. Это открыло новые возможности для информационных систем, поскольку запросы к базам данных перестали быть ограничены физическими указателями.

4.1. Формальное описание реляционной модели данных

В основе реляционной модели лежит математическое понятие теоретико-множественное отношения. Поэтому модель и получила название реляционной (от английского relation — отношение).

Рассмотрим основные понятия теории отношений.

Элементы отношения называют кортежами (или записями). Каждый кортеж отношения соответствует одному экземпляру объекта, информацию о котором требуется хранить в базе данных. Элементы кортежа принято называть атрибутами (или полями).

В основе определения отношения лежит понятие домен.

Пусть A1, A2,…, An имена атрибутов. Каждому имени атрибута Ai соответствует допустимое множество значений, которые может принимать атрибут Ai. Это множество значений Di называется доменом атрибута Ai, i =1, n . Каждый домен образует значения одного простого типа данных, например, числовые, символьные и др.. Домен может задаваться перечислением элементов, указанием диапазона значений, функцией и т.д.

Декартовым произведением k доменов D1, D2, D3,. . . Dk называется множество всех кортежей длины k, т.е. состоящих из k элементов — по одному из каждого домена и определяется следующим образом

D = D1 × D2 × D3 × … × Dk

Например, если D1 = {A, 1}, D2 = {B, C}, D3 = {2,3,D}, то k = 3 и декартово произведение равно

D = D1 × D2 × D3 = {(A, B, 2), (A, B, 3), (A, B, D), (A, C, 2), (A, C, 3), (A, C, D), (1, B, 2), (1, B, 3), (1, B, D), (1, C, 2), (1, C, 3), (1, C, D)}.

Как видно из примера, декартово произведение позволяет получить все возможные комбинации элементов исходных множеств – элементов рассматриваемых доменов.

Отношением называют некоторое подмножество декартова произведения одного или более доменов.

Например, если построить произведение трёх доменов Должности (‘директор’, ‘бухгалтер’, ‘водитель’, ‘продавец’), Оклады ( 20000 <= x <= 80000), Надбавки (1.1, 2, 3), то мы получим 4*60001*3=720012 комбинаций. Но реально отношение «Штатное расписание» содержит по одной строке на каждую должность, т.е. является именно подмножеством декартова произведения доменов.

Схемой отношения R называется перечень имен атрибутов отношения с указанием доменов этих атрибутов и обозначается

R (A1, A2, …, An); {Ai}⊆ Di ,

где {Di} – множество значений, принимаемых атрибутом Ai ( i =1, n ).

Отметим следующие свойства отношения:

Отношение имеет имя, которое отличается от имен всех других отношений.
Каждый атрибут имеет уникальное имя.
В отношении нет повторяющихся кортежей.
Значения всех атрибутов являются атомарными (неделимыми). Это следует из определения домена как множества значений простого типа данных, т.е. среди значений домена не могут содержаться множества.
Порядок рассмотрения атрибутов в схеме отношения не имеет значения, т.к. для ссылки на значение атрибута в кортеже отношения всегда используется имя атрибута.
Порядок рассмотрения кортежей в отношении не имеет значения, т.к. отношение представляет собой множество кортежей, а элементы множества, по определению теории множеств, неупорядоченны.

Значение атрибута может быть пустым, т.е. иметь значение NULL. Значение NULL приписывается атрибуту в кортеже, если значение атрибута неизвестно. Значение NULL не привязано к определённому типу данных, т.е. может назначаться данным любых типов.

Отношение имеет простую графическую интерпретацию, оно может быть представлено в виде таблицы, столбцы которой соответствуют атрибутам, а каждая строка есть кортеж. На рис. 4 приведен пример представления отношения СОТРУДНИК.

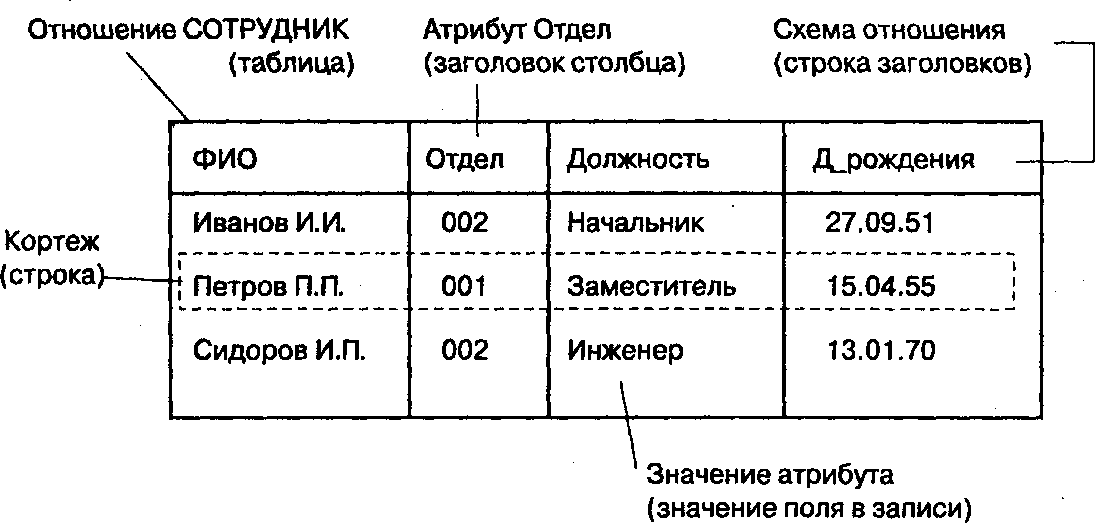
Рис. 4. Представление отношения СОТРУДНИК

В дальнейшем термины «отношение» и «таблица» будут использоваться как синонимы.

Поскольку в рамках одной таблицы не удается описать более сложные логические структуры данных из предметной области, применяют связывание таблиц.

Таким образом, реляционная база данных с логической точки зрения может быть представлена множеством двумерных таблиц самого различного предметного наполнения.

Совокупность схем отношений, используемых для представления предметной области, называется схемой реляционной базы данных.

Реляционная схема базы данных — список, в котором даются имена реляционных таблиц с перечислением их атрибутов (ключи подчеркнуты) и определений внешних ключей.

В дальнейшем каждую таблицу будем описывать следующим образом:

<ИМЯ ТАБЛИЦЫ> (<СПИСОК АТРИБУТОВ>),

где список атрибутов – это множество неповторяющихся имен атрибутов, в котором ключевые атрибуты будут выделены подчеркиванием. Например, СОТРУДНИК( ФИО, Отдел, Должность, Д_рождения) Физическое размещение данных в реляционных базах на внешних носителях легко осуществляется с помощью обычных файлов.

4.2. Ключи отношения

Одно из требований к отношению (таблицы) – это наличие в отношении ключа.

Ключ – это минимальный набор атрибутов отношения, однозначно идентифицирующий каждый из его кортежей. Минимальность означает, что исключение из набора любого атрибута не позволяет однозначно найти требуемый кортеж по значениям оставшихся атрибутов.

Каждое отношение обладает хотя бы одним ключом. Это гарантируется тем, что в отношении нет повторяющихся кортежей, а это значит, что, по крайней мере, вся совокупность атрибутов обладает свойством однозначной идентификации кортежей отношения.

Ключ, содержащий более одного атрибута, называется составным ключом.

Очень часто отношение может содержать несколько ключей, которые называют возможными (потенциальными) ключами. Один из них принимается за первичный ключ.

При выборе первичного ключа следует отдавать предпочтение несоставным ключам.

Так, для идентификации студента можно использовать либо уникальный номер зачетной книжки, либо набор из фамилии, имени, отчества, номера группы и может быть дополнительных атрибутов, так как не исключено появление в группе двух студентов с одинаковыми фамилиями, именами и отчествами.

Не допускается, чтобы первичный ключ (любой атрибут, участвующий в первичном ключе) принимал значение NULL. Иначе возникнет противоречивая ситуация, когда появится не обладающий индивидуальностью кортеж. По тем же причинам необходимо обеспечить уникальность первичного ключа.

Нецелесообразно также использовать ключи с длинными текстовыми значениями (предпочтительнее использовать целочисленные атрибуты).

Ключи обычно используют для достижения следующих целей:

исключения дублирования значений в ключевых атрибутах (остальные атрибуты в расчет не принимаются);
упорядочения кортежей. Возможно упорядочение по возрастанию или убыванию значений всех ключевых атрибутов;
ускорения работы с кортежами отношения;
организации связывания отношений.

Внешние ключи предназначены для установления связей между отношениями.

Столбец одной таблицы, значения в котором совпадают со значениями столбца, являющегося первичным ключом другой таблицы, называется внешним ключом.

Например, имеются две таблицы СТУДЕНТ(ФИО, Номер_зач_кн, Группа) и ЭКЗАМЕН(Номер_зач_кн, Дисциплина, Оценка), которые моделируют сдачу студентами экзаменационной сессии. В первой таблице первичным ключом является атрибут Номер_зач_кн. Так как каждый студент сдает несколько дисциплин в процессе сессии, то первичным ключом в таблице ЭКЗАМЕН будет набор атрибутов Номер_зач_кн, Дисциплина, т.е. ключ является составным. Оба отношения связаны через атрибуты Номер_зач_кн, которые представляют собой внешние ключи.

Внешний ключ, как и первичный, тоже может быть составным, если он ссылается на составной первичный ключ.

Если таблица связана с несколькими другими таблицами, она может иметь несколько внешних ключей.

Реляционная модель накладывает на внешние ключи ограничение для обеспечения целостности данных, называемое ссылочной целостностью. Это означает, что каждому значению внешнего ключа должны соответствовать строки в связываемых отношениях.

Кортежи отношения часто могут быть представлены внутренними номерами, которые не имеют смысла вне системы. Внутренний номер часто называют суррогатным ключом. Суррогатные ключи целесообразно использовать в следующих случаях:

естественный атрибут должен играть роль ключа, но не обладает необходимым свойством уникальности;
выбранный в качестве внешнего ключа атрибут имеет большую длину (например, длинная строка символов). Чтобы избежать его многократного дублирования, целесообразно присвоить ему код;
естественный атрибут может менять свое значение со временем, например, название предприятия или фамилия сотрудника.

4.3. Типы связи таблиц

Как уже говорилось ранее, реляционная модель представляет базу данных в виде множества взаимосвязанных таблиц (отношений). Между таблицами могут устанавливаться бинарные (между двумя таблицами), тернарные (между тремя таблицами) и, в общем случае, n-арные связи. Рассмотрим наиболее часто встречающиеся бинарные связи.

При связывании двух таблиц выделяют основную (родительскую) и подчиненную (дочернюю) таблицы. Это означает, что одна запись родительской таблицы может быть связана с одной или несколькими записями дочерней таблицы. Для поддержки этих связей обе таблицы должны содержать наборы атрибутов, по которым они связаны, т.е. внешние ключи.

В реляционных базах данных допускается три типа связи:

один – к – одному (1:1);
один – ко – многим (1 : М);
многие – ко – многим (М : М).

Тип связи определяется тем, как соотносятся первичные ключи с внешними ключами в обеих таблицах (табл. 1).

Дадим характеристику названным типам связи между двумя таблицами и приведем примеры их использования.

Связь типа 1:1

Связь один – к – одному означает, что каждая запись одной таблицы соответствует одной записи в другой таблице.

Таблица 1. Типы связи таблиц

Типы связи таблиц	1:1	1:М	М: М
Внешние ключи родительской таблицы	являются первичным ключом	являются первичным ключом	не являются первичным ключом
Внешние ключи дочерней таблицы	являются первичным ключом	не являются первичным ключом	не являются первичным ключом

В качестве примера рассмотрим две таблицы ЛИЧНОСТЬ (Код_личности, ФИО, Адрес, Телефон, Дата_рожд.) и СЛУЖАЩИЙ (Код_служащего, Должность, Квалификация (Разряд), Зарплата, Дата_поступления, Дата_уволнения). Обе таблицы содержат информацию о сотрудниках некоторой компании. В таблице ЛИЧНОСТЬ содержатся сведения о личности сотрудника, а в таблице СЛУЖАЩИЙ — профессиональные сведения. Между этими таблицами существует связь один–к–одному, поскольку для одного человека может существовать только одна запись, содержащая профессиональные сведения.

Связь между этими таблицами поддерживается при помощи внешних ключей, в качестве которых используются совпадающие поля: Код_личности (таблица ЛИЧНОСТЬ) и Код_служащего (таблица СЛУЖАЩИЙ). Отметим, что эти поля (ключи) имеют разные наименования. Связь между таблицами устанавливается на основании значений совпадающих полей, но не их наименований.

На практике связи вида 1:1 используются сравнительно редко, так как хранимую в двух таблицах информацию легко объединить в одну таблицу, которая занимает гораздо меньше места в памяти ЭВМ. Возможны случаи, когда удобнее иметь не одну, а две и более таблицы. Причинами этого может быть необходимость ускорить обработку, повысить удобство работы нескольких пользователей с общей информацией, обеспечить более высокую степень защиты информации и т. д. Приведем пример, иллюстрирующий последнюю из приведенных причин.

Пусть имеются сведения о выполняемых в некоторой организации научно-исследовательских работах. Эти данные включают в себя следующую информацию по каждой из работ: тему (полное наименование работ), шифр (код), даты начала и завершения работы, количество этапов, головного исполнителя и другую дополнительную информацию. Все работы имеют гриф «Для служебного пользования» или «секретно».

В такой ситуации всю информацию целесообразно хранить в двух таблицах: в одной из них — всю секретную информацию (например, шифр, полное наименование работы и головной исполнитель), а в другой — всю оставшуюся несекретную информацию. Обе таблицы можно связать по шифру работы. Первую из таблиц целесообразно защитить от несанкционированного доступа.

Связь типа 1 : М

Связь 1 : М имеет место в случае, когда одной записи родительской таблицы соответствует несколько записей дочерней таблицы.

Например, рассмотрим ситуацию, когда надо описать карьеру некоторого индивидуума. Каждый человек в своей трудовой деятельности сменяет несколько мест работы в разных организациях, где он работает в разных должностях. Кроме того, важно не только отследить переход работника из одной организации в другую, но и прохождение его по служебной лестнице в рамках одной организации.

Тогда мы должны создать две таблицы: СОТРУДНИК (Паспорт, Фамилия, Имя, Отчество) для моделирования всех работающих людей и КАРЬЕРА (Дата, Место работы, Должность, Номер приказа, Паспорт) для моделирования записей в их трудовых книжках.

Внешним ключом является поле Паспорт, причем в таблице КАРЬЕРА это поле не является ключевым.

Связь типа М : М

Связь много – ко – многим возникает между двумя таблицами в тех случаях, когда:

одна запись из первой таблицы может быть связана более чем с одной записью второй таблицы;
одна запись из второй таблицы может быть связана более чем с одной записью первой таблицы.

Например, преподаватель может вести занятия по разным предметам у разных студентов, а студенты, изучая разные предметы, учатся у нескольких преподавателях. Между этими двумя таблицами имеется связь типа много – ко – многим. Современные СУБД связь М : М не поддерживают. Для того, чтобы организовать такую связь необходимо использовать дополнительную таблицу – таблицу связи, которая связана с каждой таблицей, а тип связи один-ко-многим.

4.4. Манипулирование данными в реляционной модели

Основной единицей обработки данных в реляционной модели является отношение (таблица), а не отдельные его кортежи (записи) БД, и результатом обработки также является отношение. Далее полученное новое отношение может быть использовано в другой операции.

Для манипулирования данными в реляционной модели используются два формальных аппарата:

реляционная алгебра, основанная на теории множеств;
реляционное исчисление, базирующееся на исчислении предикатов первого порядка.

Оба этих аппарата лежат в основе языков манипулирования данными (ЯМД), предназначенных выполнять соответствующие операции над отношениями (таблицами) для получения информации из баз данных. Наиболее важной частью ЯМД является его раздел для формулировки запросов.

Отличаются два этих формальных аппарата уровнем процедурности. Запрос, представленный на языке реляционной алгебры, может быть реализован как последовательность элементарных алгебраических операций с учетом их старшинства и возможного наличия скобок, обеспечивающих пошаговое решение задачи. Поэтому языки реляционной алгебры являются процедурными.

Для формулы реляционного исчисления соответствующая однозначная последовательность действий, вообще говоря, отсутствует. Формула только устанавливает условия, которым должны удовлетворять кортежи результирующего отношения. Поэтому языки реляционного исчисления являются непроцедурными или декларативными. Непроцедурный язык – язык, позволяющий формулировать, что нужно сделать, а не как этого добиться.

Механизмы реляционной алгебры и реляционного исчисления эквивалентны, т.е. для любого допустимого выражения реляционной алгебры можно построить эквивалентную формулу реляционного исчисления и наоборот.

Реляционная алгебра и реляционное исчисление в настоящее время в реализациях конкретных реляционных СУБД сейчас не используется в чистом виде. Стандартом доступа к реляционным данным стал язык SQL (Structured Query Language). Тем не менее, знание алгебраических и логических основ языков баз данных часто бывает полезно на практике.

4.4.1. Реляционная алгебра

Существует много подходов к определению наборов операторов и способов их интерпретации, но в принципе все они являются более или менее равносильными. Здесь будет рассмотрен классический подход, предложенный Э. Коддом.

В этом варианте множество операторов состоит из восьми операций, составляющих две группы по четыре оператора в каждой:

традиционные операции над множествами: объединение, пересечение, вычитание и декартово произведение (все они модифицированы с учетом того, что их операндами являются отношения, а не произвольные множества).
специальные реляционные операторы: выборка, проекция, соединение и деление.

Кроме того, в состав алгебры включается операция присваивания, позволяющая сохранить в базе данных результаты вычисления алгебраических выражений. Операция присвоения является стандартной операцией компьютерного языка. Операцию присвоения будем обозначать знаками «:=».

Рассмотрим операции в том порядке, в котором они перечислены выше.

Прежде, чем говорить об операциях, введем понятие: два отношения являются совместимыми по объединению, если имеют одинаковое число атрибутов и i-атрибут одного отношения должен быть определен на том же домене, что и i-атрибут второго отношения.

Объединение (union) (R:=R1 ∪ R2)

Объединением двух совместимых по объединению отношений R1 и R2 является отношение R, включающее в себя все кортежи отношений R1 и R2 без повторов.

Например, пусть имеются отношение R1(A,B,C) (рис. 5, а) и отношение R2(A,B,C) (рис. 5, б). Тогда объединение R:=R1 union R2 будет таким, как приведено на рис. 5, в.

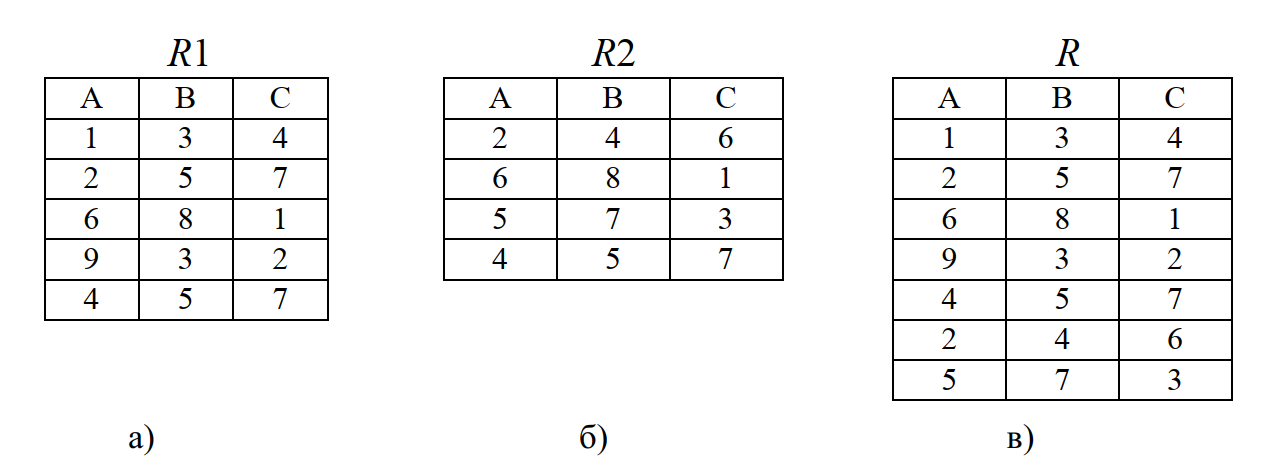
Рис. 5. Пример операции объединения

Результатом выполнения этой операции является новое отношения R, содержащее кортежи, которые принадлежат отношению R1 или отношению R2 или им обоим.

Этот пример, впрочем, как и другие примеры, подтверждает тезис о том, что с помощью одной операции реляционной алгебры решается простейшая информационная задача. Операция объединение используется для решения практической задачи – слияние файлов однотипных записей.

Заметим, что с помощью операции объединения может быть реализовано добавление новой записи к имеющемуся отношению R:=R union R2. В этом случае R – исходное отношение, R2– отношение, содержащее одну добавляемую запись.

Пересечение (intersect) (R :=R1 ∪ R2)

Пересечением двух совместимых по объединению отношений R1 и R2 является отношение R, включающее в себя все кортежи как отношения R1, так и отношения R2.

Например, пусть имеются отношение R1(A,B,C) (рис. 6, а) и отношение R2(A,B,C) (рис. 6, б). Тогда пересечение R:=R1 intersect R2 будет таким, как приведено на рис. 6, в.

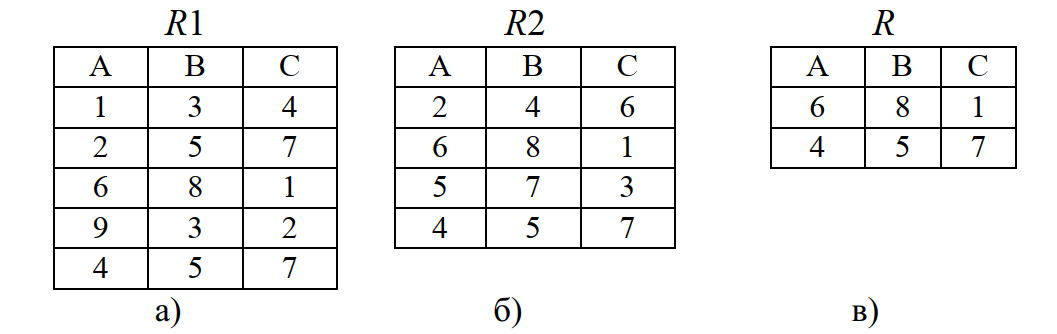
Рис. 6. Пример операции пересечения

Результатом выполнения операции пересечения будет реляционная таблица, состоящая из всех строк, встречающихся в обеих исходных таблицах. Например, если R пересечение R1 и R2: R := R1 intersect R2, то R состоит из тех строк, которые есть и в R1, и в R2.

Разность (except) (R :=R1 — R2)

Разностью двух совместимых по объединению отношений R1 и R2 является отношение R, кортежи которого принадлежат отношению R1 и не принадлежат отношению R2, т.е. кортежи отношения R1, которых нет в отношении R2.

Например, пусть имеются отношение R1(A,B,C) (рис. 7, а) и отношение R2(A,B,C) (рис. 7, б). Тогда разность R:=R1 except R2 будет такой, как приведено на рис. 7, в.

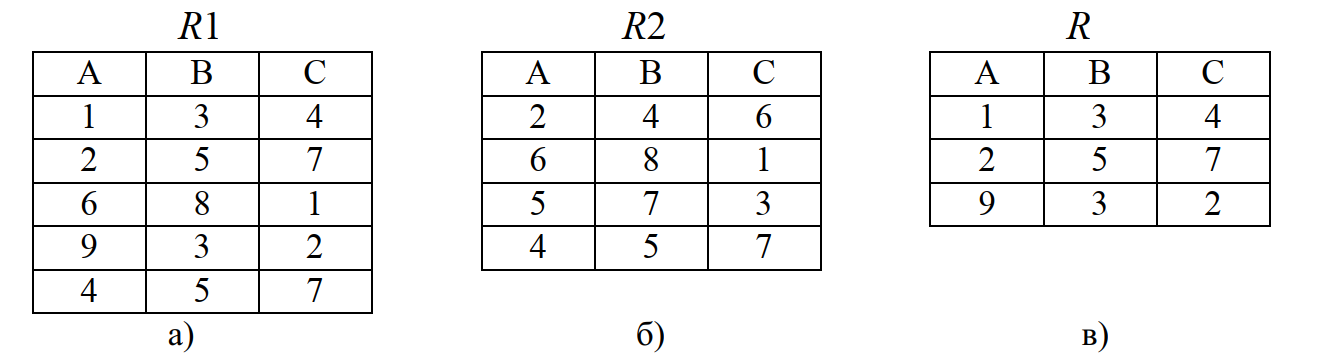
Рис. 7. Пример операции разность

Произведение (product) (R := R1 * R2)

Это бинарная операция над разносхемными отношениями.

Если отношение R1(А1, А2, …, Аm) имеет m атрибутов, а отношение R2(B1, B2, …, Bn) – n атрибутов, то произведением является отношение R(А1, А2, …, Аm, B1, B2, …, Bn), имеющее (m + n) атрибутов. Причем первые m атрибута образуют атрибуты отношения R1, а последние n атрибута – атрибуты отношения R2.

Например, пусть имеются отношение R1(A,B,C) (рис. 8, а) и отношение R2(D,E) (рис. 8, б). Тогда произведение R:=R1 product R2 будет таким, как приведено на рис. 8, в.

Следует заметить, что найти очевидные применения операции произведения практически невозможно. Операция произведения имеет большое значение в качестве составной части операции соединения, которая вероятно, является наиболее важной операцией в реляционной алгебре.

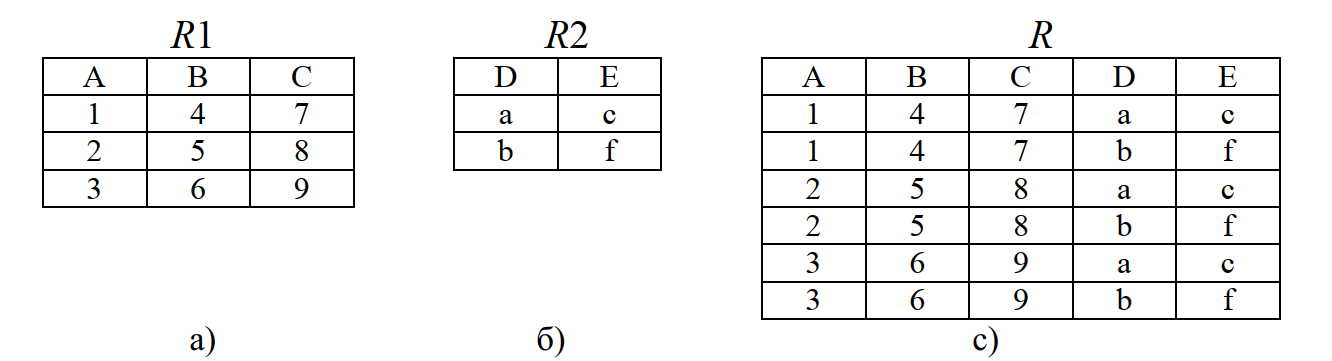
Рис. 8. Пример произведения отношений

Селекция (select) (Выборка)

Селекция – унарная операция реляционной алгебры, производящая отбор кортежей из отношения на основании некоторых условий, которые накладываются на значения определённых атрибутов.

Условия задаются логическим выражением вида «Имя атрибута — Знак сравнения – Значение», которые могут соединяться логическими операторами AND (И), OR (ИЛИ) и иметь оператор NOT (ОТРИЦАНИЕ). Знаками сравнения являются следующие знаки: =, <>, >, >=,<, <=.

В качестве примера рассмотрим отношение СКЛАД (рис. 9, а).

Нам необходима информация о диодах, хранящихся на складе, по цене меньше 2 руб. Ответ на этот запрос можно получить, выбрав из отношения СКЛАД кортежи, в которых НАИМЕНОВАНИЕ = «Диод», а значение атрибута ЦЕНА < 2.00. В реляционной алгебре это делается следующим образом:

SELECT (СКЛАД: НАИМЕНОВАНИЕ = ‘Диод’ AND ЦЕНА < 2.00)

Результатом такой выборки будет отношение, представленное на рис. 9, б.

Рис. 9. Пример операции выборка

Проекция (project)

Проекция – это унарная операция реляционной алгебры, создающая новое отношение путем исключения атрибутов из существующего отношения.

Пусть имеется отношение R1(A,B,C) (рис. 10, а). Выполним операцию проекция по атрибутам С и А. В результате получаем отношение R, представленное на рис. 10, б.

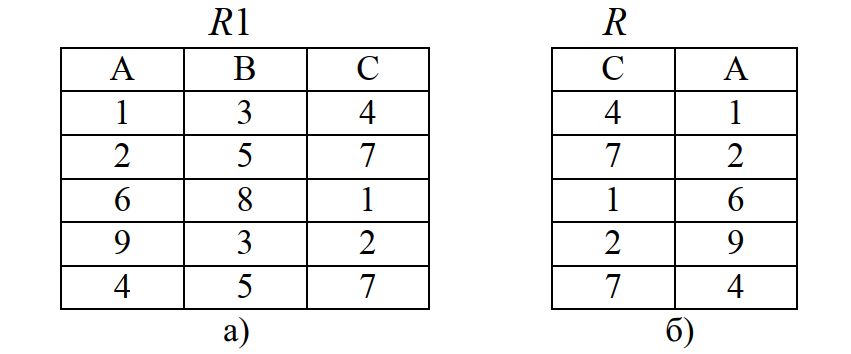
Рис. 10. Пример операции проекция

Соединение (join)

Операция соединения позволяет строить новое отношение посредством конкатенции (сцепления) кортежей двух исходных отношений. Однако канкатенция производится лишь при выполнении заданного логического условия.

Если условием является равенство значений двух атрибутов исходных отношений, такая операция называется эквисоединением. Естественным называется эквисоединение по одинаковым атрибутам исходных отношений.

Рассмотрим следующий пример. Пусть имеются отношения R1(A,B,C) (рис. 11, а) и R2(D,E) (рис. 11, б). Выполним операцию соединения этих двух отношений при условии, что значения атрибута B отношения R1 меньше значения атрибута D таблицы R2. Результат представлен на рис. 11, в.

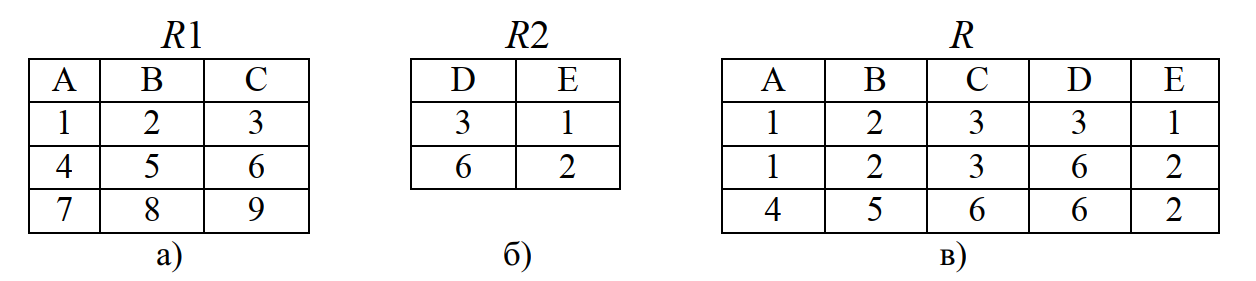
Рис. 11. Пример операции соединение

Поясним подробнее формирование записей этой таблицы. В отношении R1 значение второго атрибута (B) первого кортежа меньше значения атрибута D отношения R2 (2 < 3 и 2 < 6), поэтому формируем первые два кортежа отношения R путем объединения первого кортежа отношения R1 и соответствующих кортежей отношения R2.

Далее обрабатываем второй кортеж отношения R1. Значение второго атрибута второго кортежа отношения R1 удовлетворяет заданному условию только для второго кортежа отношения R2, поэтому формируется только один кортеж: второй кортеж отношения R1 и второй кортеж отношения R2. Третий кортеж отношения R1 не удовлетворяет заданному условию, поэтому его атрибуты и не встречаются в результирующем отношении.

Тот же результат может быть получен посредством выполнения последовательности операций произведения и выборки:

R := R1 product R2

R := SELECT (R1.B < R2.D)

Деление (division)

Операция деление в определенном смысле обратна операции произведения.

Пусть отношение R1 содержит атрибуты (A1,A2, …, Am, B1, B2,…,Bn), а отношение R2– атрибуты (B1, B2, …,Bn). Тогда результирующее отношение R содержит атрибуты (A1,A2, …, Am). Кортеж отношения R1 включается в результирующее отношение, если его декартово произведение с отношением R2 входит в R1.

Пример: пусть имеются отношения R1(A,B,C,D) (рис. 12, а) и R2(С,D) (рис. 12, б). Тогда частное R будет таким как показано на рис. 12, в.

Строка ab принадлежит R, поскольку строки abcd и abef принадлежит R1. По аналогичной причине строка ed принадлежит R. Строка bc является единственной в первых двух столбцах R1, не принадлежащая R, так как bccd не принадлежит R.

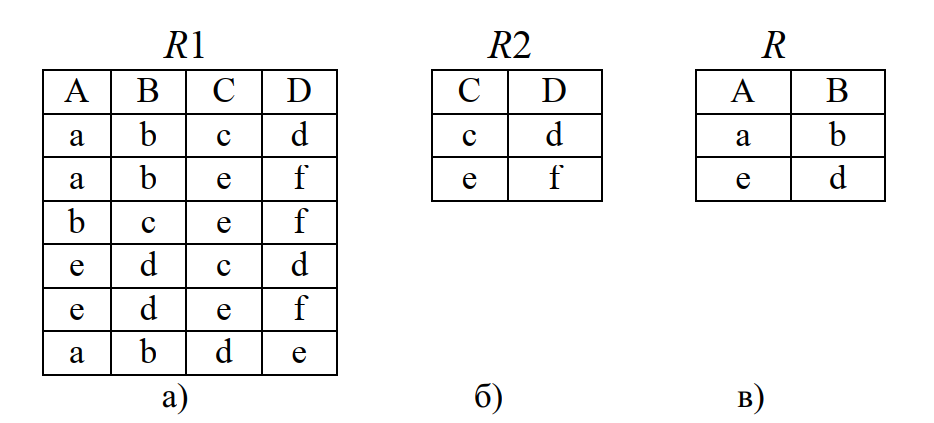
Рис. 12. Пример операции деления

4.4.2. Свойства операций реляционной алгебры

Рассмотрим основные алгебраические тождества, справедливые для операций реляционной алгебры.

Операции объединения, пересечения, произведения и соединения коммутативны, т.е. для отношений R1 и R2 справедливо:

R1 union R2 = R2 union R1;

R1 intersect R2 = R2 intersect R1; R1 product R2 = R2 product R1; R1 join R2 = R2 join R1.

Операции пересечения, объединения, произведения и соединения ассоциативны, т.е. для отношений R1, R2 и R3 справедливо:

R1 intersect (R2 intersect R3) = (R1 intersect R2) intersect R3; R1 union (R2 union R3) = (R1 union R2) union R3;

R1 product ( R2 product R3) = (R1 product R2) product R3; R1 join ( R2 join R3) = (R1 join R2) join R3.

Пары операций объединения, пересечения, произведения (или соединения) подчиняются дистрибутивным законам.

Пересечение дистрибутивно относительно объединения:

R1 intersect (R2 union R3) = (R1 intersect R2) union (R1 intersect R3).

Объединение дистрибутивно относительно пересечения:

R1 union (R2 intersect R3) = (R1 union R2) intersect (R1 union R3).

Произведение и соединение дистрибутивны относительно операций объединения и пересечения:

R1 product (R2 union R3) = (R1 product R2) union (R1 product R3); R1 product (R2 intersect R3) = (R1 product R2) intersect (R1 product R3).

Кроме этого, имеются тождества, связывающие унарные операции друг с другом и с бинарными операциями: можно заменять одну операцию несколькими более простыми и обратно. Существование алгебраических тождеств позволяет преобразовывать алгебраические выражения в эквивалентные.

Результат вычисления эквивалентных выражений будет, конечно, одинаковым, однако сложность вычисления может отличаться очень значительно (на несколько порядков). СУБД может выбрать среди эквивалентных способов записи запроса в виде выражения такой, выполнение которого требует меньшего количества вычислительных ресурсов (таких как процессорное время или количество операций обмена данными).

4.4.3. Реляционное исчисление

Так же, как и выражения реляционной алгебры, формулы реляционного исчисления определяются над отношениями, и результатом вычисления также является отношение.

Реляционное исчисление позволяет путем использования исчисления предикатов, кванторов и переменных выборки (переменныекортеж, переменные на доменах) описать отношения и операции над ними в виде аналитического выражения или формулы.

Напомним, что предикатом Р(х1, х2, …, хn) называется функция, принимающая значения “истина” или “ложь”, от аргументов, определенных в конкретных областях D1, D2, …, Dn. При построении функции используются логические операторы конъюнкция ( ∧ ), дизъюнкция ( ∨ ), отрицание, импликация (→), эквивалентность (↔). Кроме того, в функции могут использоваться термы сравнения хi Θ хj, где Θ — символ операции сравнения =, ≠, >, <, ≥, ≤.

При записи формул полезно ввести понятие “свободных” и “связанных” переменных. Вхождение переменной в формулу является “связанным”, если этой переменной предшествует квантор существования ∃ (читается некоторые, хотя бы один существует и т.п.) и квантор всеобщности ∀(читается все, всякий, каков бы ни был и т.п.). В противном случае переменную называют “свободной”. Таким образом, кванторы существования ∃ и всеобщности ∀ позволяют отнести формулу ко всему рассматриваемому множеству. Так выражение

∃ х( f(x) > a) означает, что среди элементов множества Х найдется по крайней мере один, при котором оказывается истинным неравенство, заключенное в скобках. Если использовать квантор всеобщности ∀ х( f(x) > a), то получим высказывание: для всех элементов множества Х некоторая функция f(x) больше заданного значения а.

В реляционном исчислении принято связывать с отношением R(A1, A2, …, An) некоторый предикат Р(х1, х2, …, хn), аргументы которых имеют одинаковые области определения, таким образом, что если Р(а1, а2, …, аn) = 1, то кортеж (а1, а2, …, аn) принадлежит отношению

R. В противном случае кортеж не входит в состав указанного отношения. Отсюда следует, что посредством задания некоторого предиката может быть задано и соответствующее ему отношение.

Пример построения отношения с помощью реляционного исчисления. Пусть задано отношение R1(A1, A2) (рис. 13, а).

Поставим отношению R1 в соответствие предикат Р1: R1(A1, A2)↔ Р1(х1, х2), где переменные х1 и х2 имеют области определения A1 и A2. Тогда предикат Р2(х1) ↔ ∀ х2 Р1(х1, х2) ∧ (х2 > 2) формирует новое отношение R2(A3), в которую войдут лишь те значения х1, для которых соответствующие значения х2 в отношение R1 оказались больше 2 (рис. 13,б).

Рис. 13. Пример создания отношения с помощью реляционного исчисления

Таким образом, реляционное исчисление позволяет записывать различного вида запросы и создавать новые отношения.

Следует отметить, что между реляционной алгеброй и реляционным исчислением существует тесная связь. Это означает, что любой запрос, который можно сформулировать при помощи логического исчисления, также можно сформулировать, пользуясь реляционной алгеброй, и наоборот. Так операцию объединения R:=R1 union R2 эквивалентно можно записать следующим образом R1 ∨ R2, а операцию разность R :=R1 except R2 как R1 ∧ ¬ R2.

Рассмотренные языки реляционной алгебры и реляционного исчисления служат основой реальных языков манипулирования данными реляционных БД. По своим выразительным способностям эти языки эквивалентны друг другу. Однако языки исчисления – это непроцедурные языки, так как их средствами описать лишь свойства желаемого результата, не указывая, как его получить. Выражения реляционной алгебры, напротив, специфицируют конкретный порядок выполнения операций. При этом пользователь должен сам выполнить оптимизацию своего запроса при его формулировке.

Пример. Пусть даны два отношения:

СОТРУДНИКИ (сотр_номер, сотр_имя, сотр_зарпл,отд_номер),

ОТДЕЛЫ(отд_номер, отд_кол, отд_нач).

Здесь атрибут отд_кол означает количество сотрудников в отделе, а отд_нач – фамилию начальника отдела. Мы хотим узнать имена и номера сотрудников, являющихся начальниками отделов с количеством работников более 10. Выполнение этого запроса средствами реляционной алгебры распадается на четко определенную последовательность шагов:

Выполнить соединение отношений СОТРУДНИКИ и ОТДЕЛЫ по условию сотр_номер = отдел_нач:
Из полученного отношения произвести выборку по условию отд_кол > 10:
Получить проекцию результатов предыдущей операции на атрибуты сотр_имя, сотр_номер:

Заметим, что порядок выполнения шагов может повлиять на эффективность выполнения запроса. Так, время выполнения приведенного выше запроса можно сократить, если поменять местами этапы 1 и 2. В этом случае сначала из отношения СОТРУДНИКИ будет сделана выборка всех кортежей со значением атрибута отдел_кол > 10, а затем выполнено соединение результирующего отношения с отношением ОТДЕЛЫ. Машинное время экономится за счет того, что в операции соединения участвуют меньшие отношения.

На языке реляционного исчисления данный запрос может быть записан как:

выдать сотр_имя и сотр_ном для СОТРУДНИКИ таких, что существует ОТДЕЛ с таким же, что и сотр_ном значением отд_нач и значением отд_кол большим 10.

Здесь мы указываем лишь характеристики результирующего отношения, но не говорим о способе его формирования. СУБД сама должна решить, какие операции и в каком порядке надо выполнить над отношениями СОТРУДНИКИ и ОТДЕЛЫ. Задача оптимизации выполнения запроса в этом случае также ложится на СУБД.

В общем случае языки манипулирования данными содержат операции, выходящие за рамки возможностей реляционной алгебры и реляционного исчисления. Это прежде всего команды: добавить данные, модифицировать данные, удалить данные. Кроме этих операций обычно представляются и другие дополнительные возможности, например, в формулы реляционного исчисления и операции реляционной алгебры (операции выбора) могут включаться арифметические вычисления.

4.5. Достоинства и недостатки реляционной модели данных

Достоинство реляционной модели данных заключается в простоте, понятности и удобстве физической реализации на ЭВМ. Именно простота и понятность для пользователя явились основной причиной их широкого использования. Проблемы же эффективности обработки данных этого типа оказались технически вполне разрешимыми. В качестве основного недостатка реляционной модели можно указать дублирование информации для организации связей между таблицами.

Например, база данных имеет следующую схему:

R1(A1, A2, A3, A4)

R2(A5, A6)

R3(A7, A8)

R4(A1, A5)

R5(A1, A7)

R6(A5, A7),

где R1, R2, R3, R4, R5, R6 – это таблицы, а A1, A2, A3, A4, A5, A6, A7 – это атрибуты таблиц. Не трудно заметить, атрибуты А1, А5, А8 присутствуют в нескольких таблицах.

Отсутствие специальных механизмов навигации (как в иерархической или сетевой моделях), с одной стороны, ведёт к упрощению модели, а с другой – к многократному увеличению времени на извлечение данных, т.к. во многих случаях требуется просмотреть всё отношение для поиска нужных данных.

Не смотря на указанные недостатки, реляционная модель данных широко используется в теории и практики баз данных.

4.6. Ограничения целостности базы данных

Важной компонентой реляционной базы данных являются ограничения целостности базы данных.

В процессе работы с базой данных значения атрибутов отношений и экземпляры связей между ними могут меняться во времени. Поэтому в любой момент реляционная база данных содержит некоторую определенную конфигурацию данных, и эта конфигурация должна отражать реальную действительность (целостность данных).

Следовательно, определение базы данных нуждается в расширении, включающем правила целостности данных, назначение которых в том, чтобы информировать СУБД о разного рода ограничениях реального мира.

Примерами правил целостности могут быть:

количество продаваемого товара должно быть больше 0;
номер паспорта является уникальным значением;
возраст принимаемого сотрудника на работу обязательно не меньше 14 лет.

Фактически ограничения целостности – это правила, которым должны удовлетворять значения данных в БД. Учесть их это задача разработчика БД. Ограничения целостности включаются в структуру базы данных с помощью средств языка SQL.

За выполнением ограничений целостности следит СУБД в процессе своего функционирования. Она проверяет ограничения целостности каждый раз, когда они могут быть нарушены (например, при добавлении данных, при удалении данных и т.п.), и гарантирует их соблюдение. Если какая-либо команда нарушает ограничение целостности, она не будет выполнена и система выдаст соответствующее сообщение об ошибке. Например, если задать в качестве ограничения правило «Остаток денежных средств на счёте не может быть отрицательным», то при попытке снять со счёта денег больше, чем там есть, система выдаст сообщение об ошибке и не позволит выполнить эту операцию. Таким образом, ограничения целостности обеспечивают логическую непротиворечивость данных при переводе БД из одного состояния в другое.

Более сложные правила целостности реализуются с помощью хранимых процедур и триггеров, представляющие определенные последовательности команд языка SQL при изменении или добавлении данных в БД.

Post Views: 788

1. Компоненты даталогических моделей данных